前天在一次面试中，面试官问到我汉诺塔(Towers of Hanoi)的问题，当时只知道是递归，知道手动玩游戏怎么玩，写程序还真的忘记了。大学我记得是有写过这样的作业，还有八皇后等等，不过真的都还给老师了，哈哈哈！
然后回家看了下，
http://www.cs.cmu.edu/~cburch/survey/recurse/hanoiimpl.html
http://www.python-course.eu/towers_of_hanoi.php
汉诺塔的介绍参见http://en.wikipedia.org/wiki/Tower_of_Hanoi等等
程序如下，
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | #include <stdio.h>void move(char src, char dest){ printf("\nMove the top plate of %c to %c", src, dest);}void hanoi(int n, char a, char b, char c){ if (n == 1) { // 递归结束 move(a, c); // 最小的那个盘子 } else { hanoi(n - 1, a, c, b); // step 1，把所有小于最大的盘子移动到临时的柱子上(可以借助目的柱子) move(a, c); // step 2，把最大的盘子移动到目的柱子上 hanoi(n - 1, b, a, c); // step 3，把临时的柱子上的盘子移动到目的柱子上(可以借助原始柱子)，和step 1的方式一模一样 // step 1和3都会有递归产生 }}int main(){ int n; printf("\nPlz input number of the plates:"); scanf("%d", &n); printf("\nMoving %d plates from A to C:", n); hanoi(n, 'A', 'B', 'C'); printf("\nDone!\n");} |
如果你能看懂上面的注释，很好。如果你看不懂，也没关系，现在我们来试着详细点解释这个问题。
我们先来玩这个游戏，如图(点击图片看正常大图)，
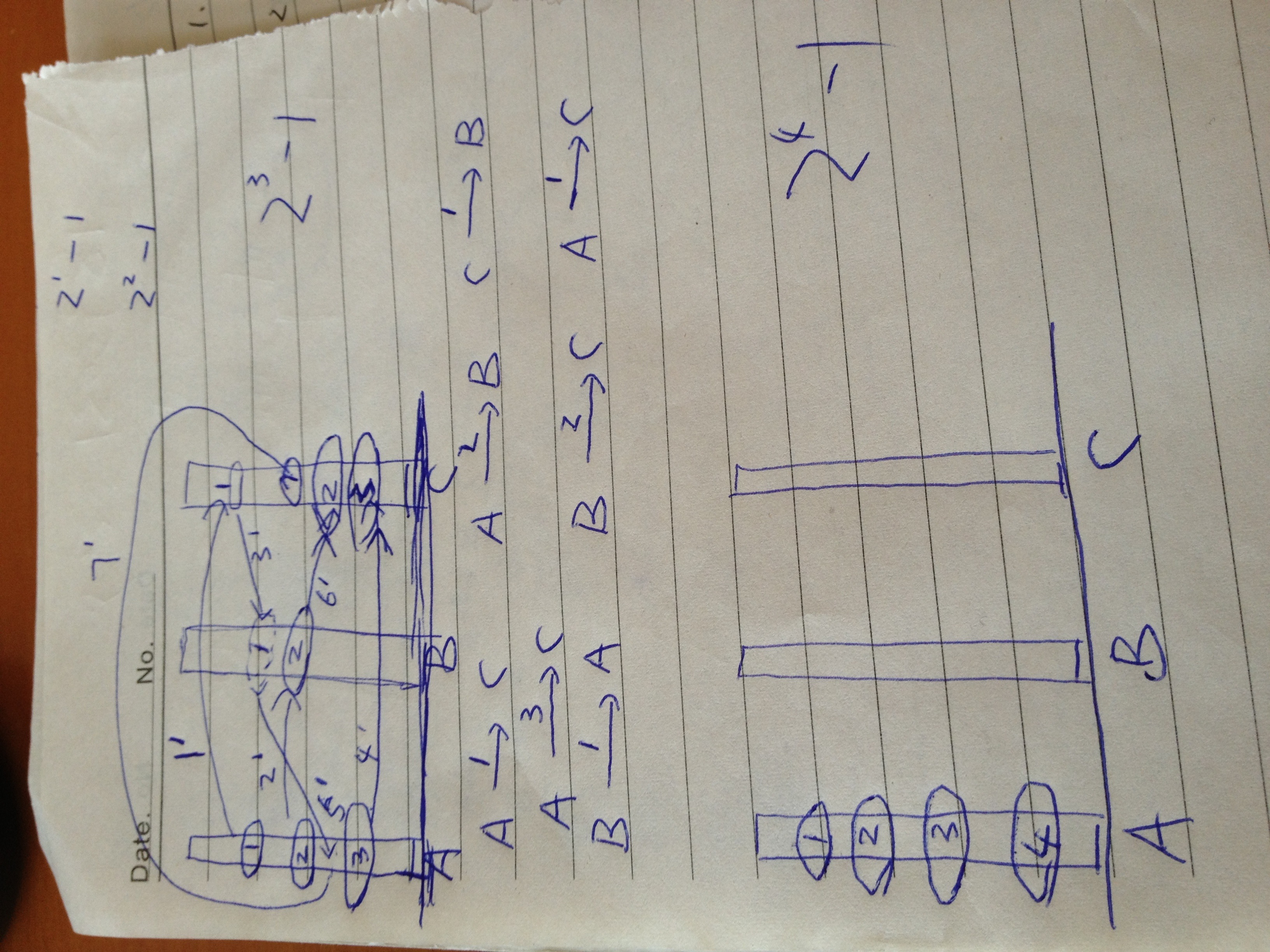
你会发现盘子的数量和最终要花费的步数是有关系的，为2^n – 1，也就是说只有1个盘子的时候需要1步，2个盘子的时候需要3步，3个盘子的时候需要7步，以此直到天荒地老。。。
所以这种思路我们是不是可以采用递归那完成呢？
比如3个盘子的时候，我们先移动上面的2个盘子(需要3步)，再移动最大的1个盘子(需要1步)，然后再移动那2个盘子到最大的盘子上面(需要3步)，加起来一共就是7步，刚刚好。
并且2个盘子也可以同理拆分，最终会变成1个盘子的情况，1个盘子的情况很好解决，就1步，别且这也就是边界情况。
看起来这样是可以，再回头来看看程序，
step 1 ~ 3是不是很清晰了，并且step 1和3自己又会有递归产生，继续拆分，直到最后都是1个盘子的时候，递归结束。
如果不关心内部细节是不是就这样完美结束了呢？确实，如果你不关心内部细节，这样已经让人很容易的理解这个问题。但是总归会有一部分人会继续深挖。
现在我们以3个盘子为例，以程序执行的角度来看，
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | hanoi(3, 'A', 'B', 'C'){ hanoi(2, 'A', 'C', 'B'); hanoi(1, 'A', 'B', 'C') move('A', 'C') move('A', 'B') hanoi(1, 'C', 'A', 'B') move('C', 'B') move('A', 'C'); hanoi(2, 'B', 'A', 'C'); hanoi(1, 'B', 'C', 'A') move('B', 'A') move('B', 'C') hanoi(1, 'A', 'B', 'C') move('A', 'C')} |
好像也没什么好写的，有机会看看非递归的方式来实现。
P.S.
递归有风险，使用需谨慎！